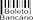Testing and Analyzing D’Alembert Roulette System

Last updated: 03.29.2024 by Andrew Shepard

The d'Alambert system is very popular among roulette strategy reviewers: if you have a quick search on Google, you will find out that almost all articles write about it, and describe it as an effective stratagem. Yet, most such explanations seem to lack a fair bit of explanation or even justification. We have decided to take matters in our own hands, though, and explain what d’Alembert is as a strategy and whether it brings any tangible benefit to your roulette gameplay. The strategy was invented by Jean le Rond d'Alembert in the 1800s and has been put to good use in roulette gameplay ever since.

How does d'Alembert work?

Everything is simple. All bets are calculated on even money bets (red/black, even/odd, higher/lower). For the purposes of testing, we took a base unit, for example, $5. If we win, we lower the base bet by $5; if we lose, we raise the next bet by $5. And so every move. It is usually recommended to make sure your base unit does not exceed 1% of the bankroll. If the rate cannot be reduced below the base rate, then we take the base rate. The strategy is somewhat reminiscent of Martingale, but here the dynamics will not be so sharp.

Now, for clarity, refer to the following example of what a d’Alembert strategy may look like:

Example

Spin 1
We bet $5, and we win. We do not raise or lower the bet as we have just started.
Spin 2
We bet $5, and we lose. Now, we double the bet.
Spin 3
We bet $10, and we lose. We increase the bet by $5.
Spin 4
We bet $15, and we win. We reduce the bet.
Spin 5
We bet $10, and we win. We reduce the bet again.

Our test of d'Alembert system

Now let's test this strategy. Since it is a simple progression, we will use the move simulator we developed and use the specific formula in Google Sheets. Let's take a bankroll of $500 for the first player and an initial bet of $5. We want to start the game and set it at 500 spins.

The result is quite interesting. It can be seen that the value of the bet grows with the flow of the game: if you started with $5, then at the time the bankroll went down to $70, it was already $115. This is because the bet increases when you lose; according to statistics, there are fewer losses. When the player got to move 350, his progression came to a standstill, so the next move would have required a bet of $115, leaving $70 in the bankroll.

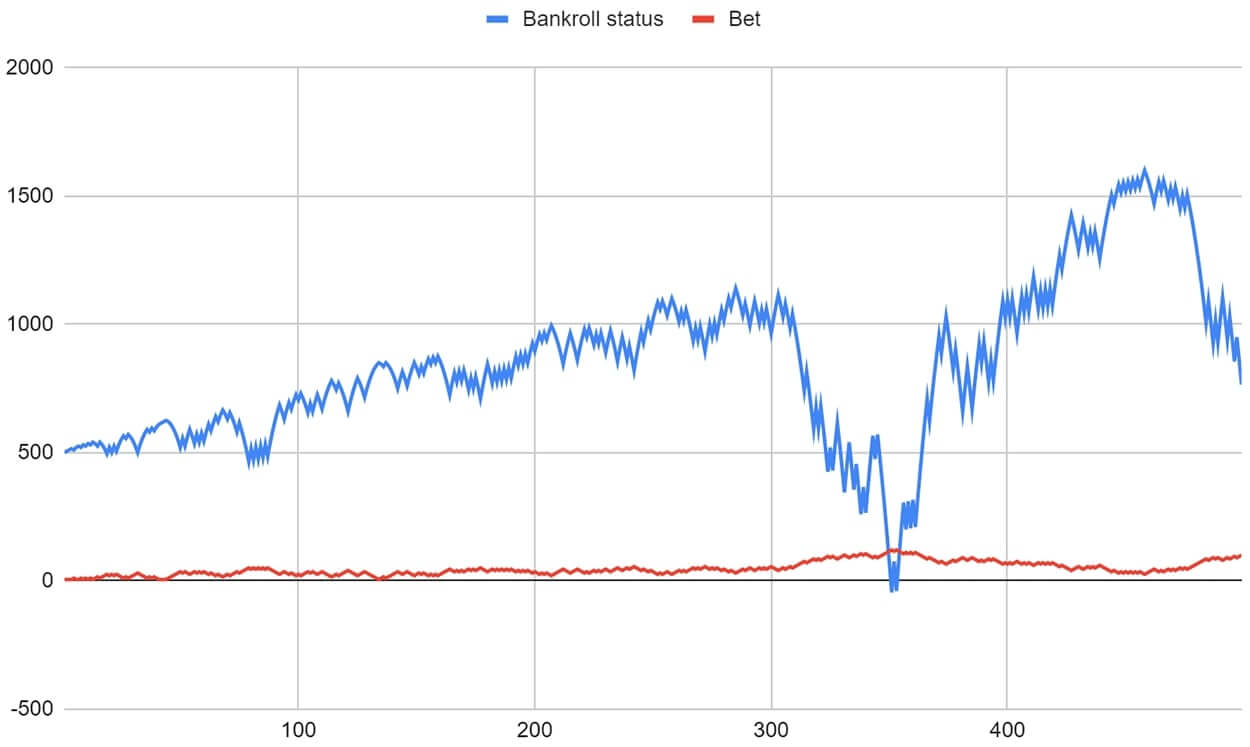
So let's see the second player with a $10 starting bet and a $1000 bankroll:

Here the player's progression came to a standstill at move 251, and then we took him out of the game with a bankroll of $81.

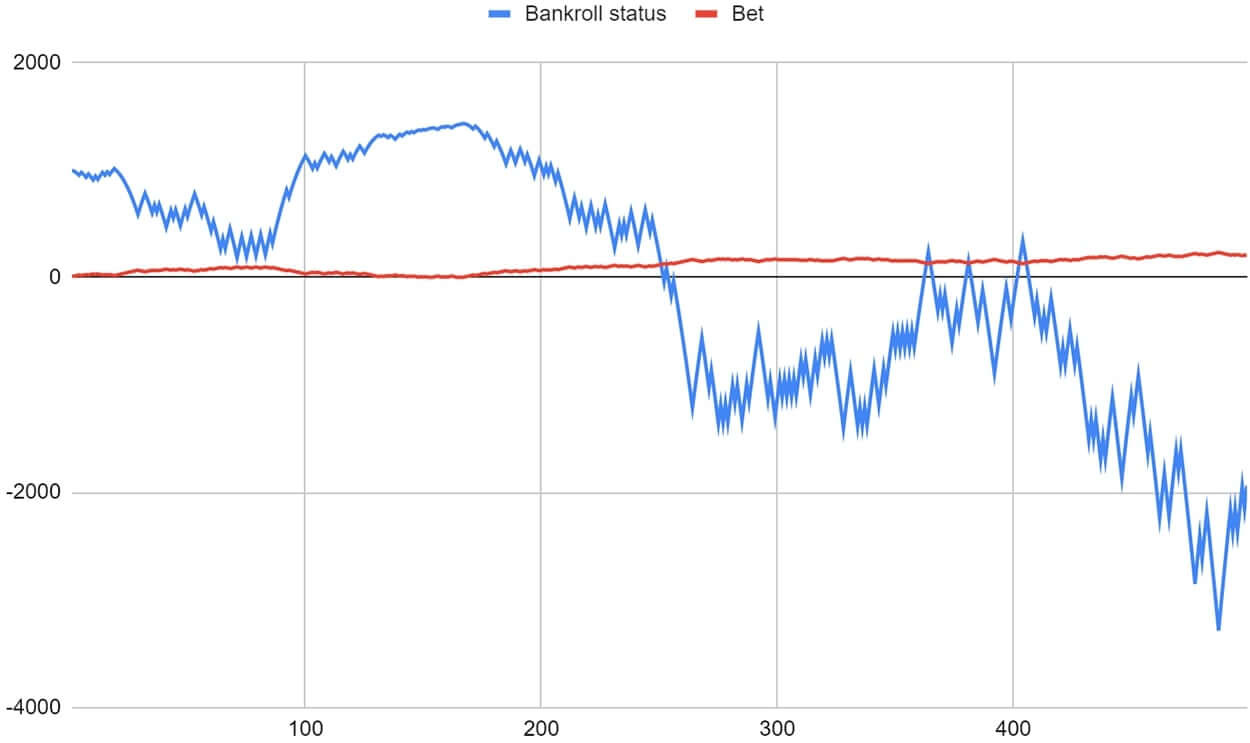
To diversify the experiment, let's run the third player with a bankroll of $1000 and a base bet of $5

This time we don't see any bankroll dips, and here we end with a profit, with a bankroll of $2130. But it cannot be said that, in this case, the success of the progression is because the rate was lowered. This is pure coincidence. We tried different initial bets, and the results of the games came out very diverse. Besides, a bankroll of $1000 also offers some better opportunities.

What is remarkable is that when launching different players, we observed both positive and negative general trends in the bankroll state. At the same time, it can be seen that the larger the bet, the more dynamic the bankroll becomes.

Explanation of pitfalls and when betting d'Alembert

This strategy is not as risky as Martingale, but you need to consider the following:

As the game progresses, the rate will gradually increase, which means that the risk of bankroll collapse will increase at such moments. At the same time, it is also an opportunity to recoup faster.
Since the algorithm is an arithmetic progression, it will take many moves for a tangible result. It can be a hundred or more. In real play conditions, not everyone has such a resource of time.

Conclusion

Testing d'Alembert's strategy showed that, in general, game scenarios could be very different and unpredictable, even though a simple arithmetic progression is taken as the basis. We see that the overall trend of the bankroll during a long game can be both positive and negative.

In general, the course of the game is influenced by the fact that the value of the bet will slowly increase during the game. The more bets are, the more dynamic the game will be and the bankroll state, too. This is seen in the resulting graphs. On the other hand, if we consider that players are unlikely to use this strategy for several hundred moves in real conditions, then the bet increase will be less noticeable than in our experiments.

In general, we can say that the strategy is relatively safe; you will not be able to lose a lot of money sharply. On the other hand, you will also not win a lot sharply. The process of the game can be accompanied by both smooth falls and smooth growth.

The pitfall is the growth of the bet with the course of the game - for example, the dynamics of the growth or fall of the bankroll increases sharply. Hence more risk.

From a practical point of view, it certainly doesn't make sense to play this strategy indefinitely. You will have to play for a long time, but here it is important to stop at the right time. That is when you have raised a certain amount of funds that nets you a gain. Otherwise, the rise will sooner or later be followed by a fall.

Your new strategy is waiting to be tested - play roulette for real!

1

Wild Casino
5/5

Accepts US players

Bonus 100% up to $5 000

Wagering requirement x25

Roulette games 10+

Live dealer
Payments
Play now Read Review
2

DuckyLuck
5/5

Accepts US players

Bonus 500% up to $2 500

Wagering requirement x30

Roulette games 5

Live dealer
Payments
Play now
3

Jackbit Casino
5/5

Accepts US players

Rakeback up to 30%+ 100 Freespins

Wagering requirement x1

Roulette games 40+

Live dealer
Payments
Play now
4

BetUS
5/5

Accepts US players

Bonus 100% up to $3 000

Wagering requirement x30

Roulette games 10+

Live dealer
Payments
Play now Read Review
5

Ignition Casino
5/5

Accepts US players

Bonus 100% up to $2 000

Wagering requirement x25

Roulette games 10+

Live dealer
Payments
Play now Read Review
6

BetOnline
5/5

Accepts US players

Bonus 100% up to $1 000

Wagering requirement x30

Roulette games 10+

Live dealer
Payments
Play now Read Review
7

SlotoCash
5/5

Accepts US players

Bonus 100% up to $1 000

Wagering requirement x25

Roulette games 5+

Live dealer
Payments
Play now Read Review
8

BoVegas
4.9/5

Accepts US players

Bonus 100% up to $5 500

Wagering requirement x60

Roulette games 5+

Live dealer
Payments
Play now Read Review
9

Coinsgame
4.8/5

Accepts US players

Bonus 180% up to $20 000

Wagering requirement x20

Roulette games 10+

Live dealer
Payments
Play now
10

SlotsEmpire
4.7/5

Accepts US players

Bonus 245% Welcome offer

Wagering requirement x35

Roulette games 5+

Live dealer
Payments
Play now Read Review
11

BC.Game
4.7/5

Accepts US players

Bonus 180% up to $20 000

Wagering requirement x40

Roulette games 20+

Live dealer
Payments
Play now
12

Red Dog
4.5/5

Accepts US players

225% welcome bonus code: WAGGINGTAILS

Wagering requirement x35

Roulette games 5+

Live dealer
Payments
Play now Read Review
13

Golden Lion
4.5/5

Accepts US players

$75 Roulette Match code: TALISMAN75

Wagering requirement x60

Roulette games 5+

Live dealer
Payments
Play now Read Review
14

El Royale
4.5/5

Accepts US players

260% welcome bonus code: TRUEROYAL

Wagering requirement x35

Roulette games 5+

Live dealer
Payments
Play now Read Review