Testing and Analyzing Grand Martingale System

Last updated: 03.29.2024 by Andrew Shepard

The Grand Martingale system is a variation of the classic Martingale. If you are not familiar with the latter, then, first of all, we recommend that you familiarize yourself with it in our article. The difference is that if you lose, the bet is doubled, and the baseline is also added, pushing the progression further up. It is logical to assume that the passage will pick up much quicker when compared to the original strategy, i.e., Martingale. This system has historically been used to win back lost bets faster. However, by increasing the base bet to recoup potential losses, you are also increasing the chance of running out of betting limits and losing money quicker. Let’s see how this strategy works in practice and what the mathematical justification for it is.

How does Grand Martingale work? Algorithm Explanation

Like Martingale, players will bet on even money bets such as Black/Red, Odd/Even, High/Low, and so on. A conditional minimum bet is set at the start, for example, $1. If we lose, we double the bet and add the base bet ($1). If we win, we return to the baseline. So, how does this system work in practice?

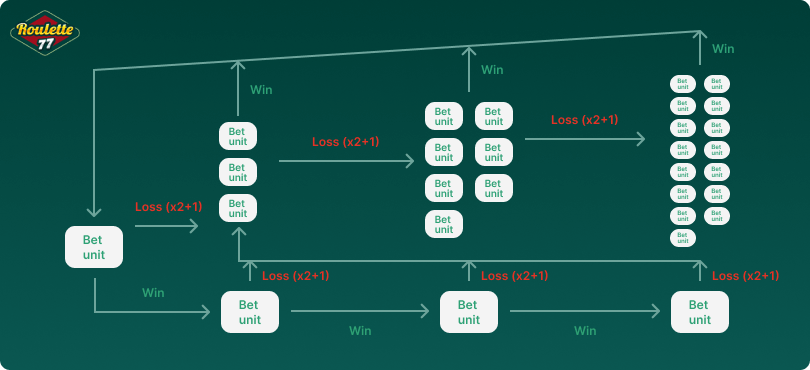
A quick example of it will have you do the following:

Example

Spin 1
Base bet 1$ on Black. Let's tell we lost.
Spin 2
We doubled and added the base bet (2$+1$=3$). So, bet 3$ on Black. For example, we lose again.
Spin 3
Double the lost bet and add the baseline (6$+1$=7$). Bet 7$ on black again, and here we win. With this win, we made up for our losses, so back to the base bet for the next spin.
Spin 4
Bet 1$ on Black and according to outcome(win or lose) proceed with the algorithm

Our test of Grand Martingale system

Just like for our Martingale test, we will use our random number generator and betting simulator programmed in Google Sheets. Similarly, let's take 3 players and give each player $1000. We adjust the formula for Grand Martingale and launch the game of 1000 spins. As a result, we get the following graph.

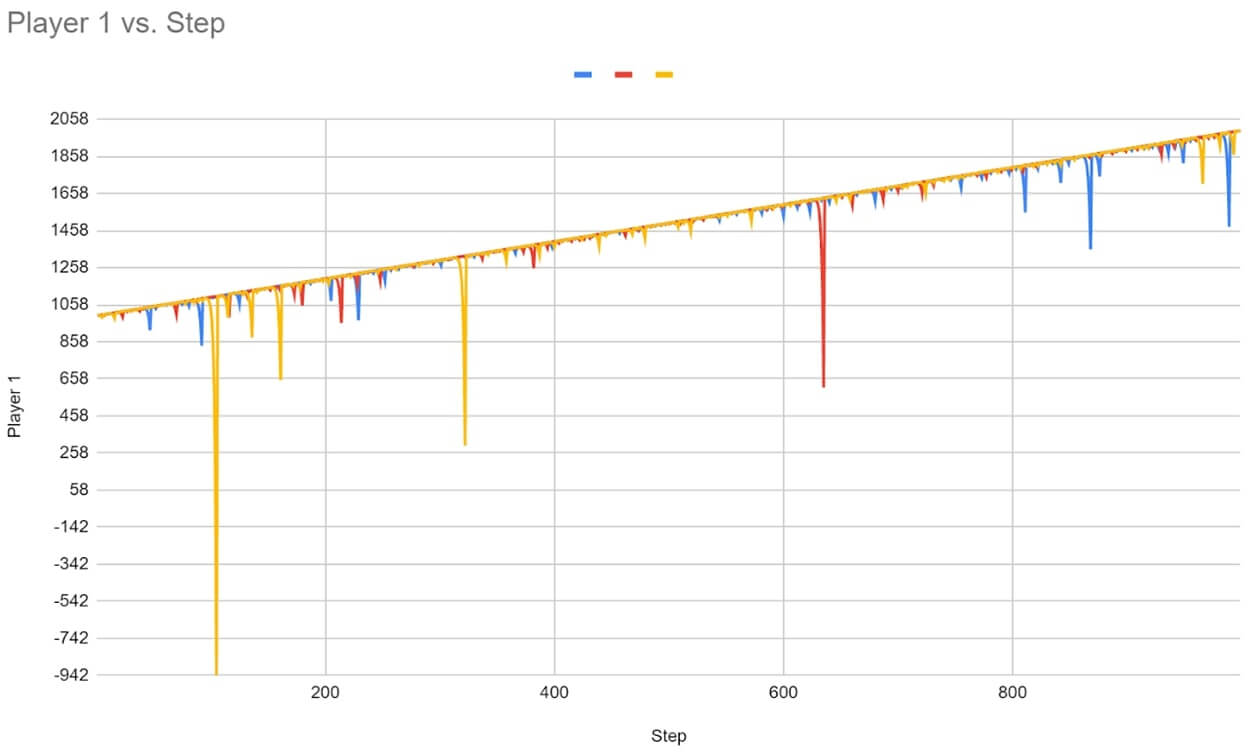
The first player turned out to be the most successful, his progression lasted until the last round, and he finished the game with a bankroll of $1998. Player 2's progression broke on spin 636. His bankroll dropped to $612, and he would have needed to bet $1023 to continue the progression, but this amount is lower than his bankroll. And the third player lowered the budget to $81 on the 104th spin and did not have enough funds to restore the bankroll by the subsequent doubling of the bet.

Now, for comparison, let's run two players under the same conditions. Only one will play according to Martingale, and the other according to Grand Martingale:

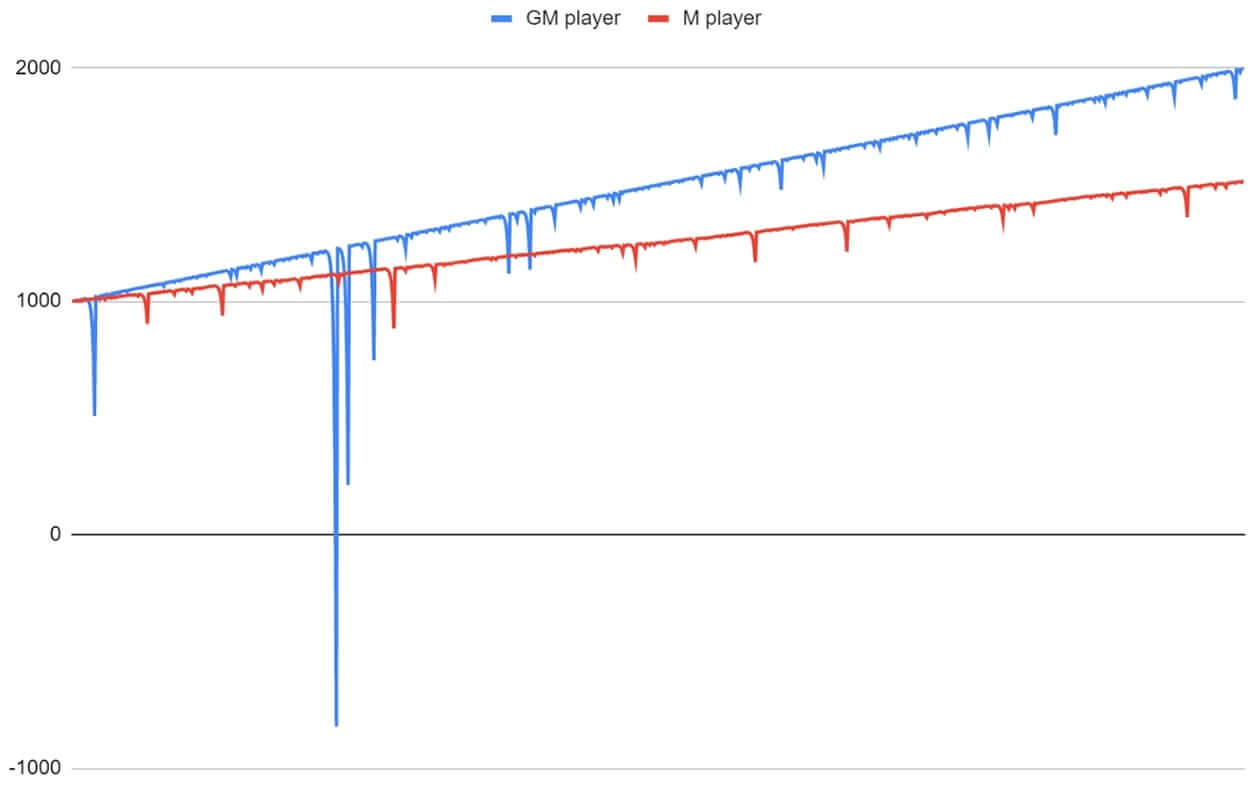
As expected, it is clear that the progression of Grand Martingale is going much faster. The first player in Grand Martingale failed on the 21st spin, knocking down the bankroll to $509. And the Martingale player was lucky, reaching the end with a balance of $1513.

We see that the money progressively accumulates approximately 35% faster with Grand Martingale. But at the same time, the risks of reaching an unrecoverable bankroll are higher. For example, for Martingale, the following sequence of losses will be critical:

1 - 2 - 4 - 8 - 16 - 32 - 64 - 128 - 256 - 512 - if the initial bankroll is $1000, then there will not be enough money for the 10th bet of $512

Similarly, for the Grand Martingale:

1 - 3 - 7 - 15 - 31 - 63 - 127 - 255 - 511 - here, again, $511 is not enough for a bet, but the number of allowed consecutive losses is reduced by 1.

Let's see how the probability of such a failure, according to Martingale, is if we play European Roulette:

P = (0.524)^10 = 0.1275%

For Grand Martingale:

P = (0.524)^9 = 0.2433%

Explanation of pitfalls and when betting Grand Martingale

In general, all the weak points of this system are the same as those of the classic Martingale, namely the betting limits and the ever-present chance of running out of bankroll to support your gameplay through the game's later stages (or sometimes even sooner). Moreover, since this is a more aggressive version of the Martingale, the risk of going beyond the limits and the bankroll is two times higher.

Conclusion

The Grand Martingale is a more aggressive version of the Martingale: the progression grows 35% faster on average because when the bet is doubled, the initial bet is added on top. Plus, you can win back what has been lost in fewer steps, so the probability of going beyond the limits or the bankroll increases by double the average rate.

Many may not like Classic Martingale because to win at least a substantial amount. You must successfully go through many moves where you keep sticking painstakingly to the algorithm. To speed things up a little, they resort to the Grand Martingale.

Those who do not like Martingale will not like this system either. It will not suit you if you have a small bankroll (everything is relative, but let's say $100 is small), low betting limits, or limited time to play. On the other hand, you can, for example, in some cases, say, increase the initial bet a little more, $2-$5, to win back the losses as quickly as possible. After all, the main thing is to understand in what cases you can use one strategy or the other and not play the game, misunderstanding the strategy or acting impatiently, hurting your chances of winning as you do.

Your new strategy is waiting to be tested - play roulette for real!

1

Wild Casino
5/5

Accepts US players

Bonus 100% up to $5 000

Wagering requirement x25

Roulette games 10+

Live dealer
Payments
Play now Read Review
2

DuckyLuck
5/5

Accepts US players

Bonus 500% up to $2 500

Wagering requirement x30

Roulette games 5

Live dealer
Payments
Play now
3

Jackbit Casino
5/5

Accepts US players

Rakeback up to 30%+ 100 Freespins

Wagering requirement x1

Roulette games 40+

Live dealer
Payments
Play now
4

BetUS
5/5

Accepts US players

Bonus 100% up to $3 000

Wagering requirement x30

Roulette games 10+

Live dealer
Payments
Play now Read Review
5

Ignition Casino
5/5

Accepts US players

Bonus 100% up to $2 000

Wagering requirement x25

Roulette games 10+

Live dealer
Payments
Play now Read Review
6

BetOnline
5/5

Accepts US players

Bonus 100% up to $1 000

Wagering requirement x30

Roulette games 10+

Live dealer
Payments
Play now Read Review
7

SlotoCash
5/5

Accepts US players

Bonus 100% up to $1 000

Wagering requirement x25

Roulette games 5+

Live dealer
Payments
Play now Read Review
8

BoVegas
4.9/5

Accepts US players

Bonus 100% up to $5 500

Wagering requirement x60

Roulette games 5+

Live dealer
Payments
Play now Read Review
9

Coinsgame
4.8/5

Accepts US players

Bonus 180% up to $20 000

Wagering requirement x20

Roulette games 10+

Live dealer
Payments
Play now
10

SlotsEmpire
4.7/5

Accepts US players

Bonus 245% Welcome offer

Wagering requirement x35

Roulette games 5+

Live dealer
Payments
Play now Read Review
11

BC.Game
4.7/5

Accepts US players

Bonus 180% up to $20 000

Wagering requirement x40

Roulette games 20+

Live dealer
Payments
Play now
12

Red Dog
4.5/5

Accepts US players

225% welcome bonus code: WAGGINGTAILS

Wagering requirement x35

Roulette games 5+

Live dealer
Payments
Play now Read Review
13

Golden Lion
4.5/5

Accepts US players

$75 Roulette Match code: TALISMAN75

Wagering requirement x60

Roulette games 5+

Live dealer
Payments
Play now Read Review
14

El Royale
4.5/5

Accepts US players

260% welcome bonus code: TRUEROYAL

Wagering requirement x35

Roulette games 5+

Live dealer
Payments
Play now Read Review